亲爱的读者,今天我要和你聊聊一个数学中的小秘密——指数函数求导。你可能觉得这听起来有点枯燥,但别急,我会用最简单的方式,让你对这个概念爱不释手。
指数函数求导的奇妙之旅

想象你手中有一只神奇的兔子,每天都会变成两只。第一天,你只有一只兔子;第二天,它变成了两只;第三天,变成了四只;第四天,八只……这样的增长,是不是很神奇?这就是指数函数的魅力。
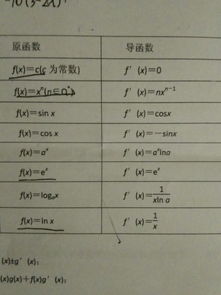
指数函数的数学表达式通常是 f(x) = a^x,其中 a 是一个大于0且不等于1的常数,x 是自变量。现在,让我们来看看如何求导这个函数。
指数函数求导的奥秘

首先,我们要知道指数函数的求导公式:f'(x) = a^x ln(a)。这里的 ln(a) 是以自然对数为底 a 的对数。
这个公式是怎么来的呢?其实,它是通过极限的方法推导出来的。不过,你不需要知道具体的推导过程,只需要记住这个公式就可以了。
指数函数求导的实际应用
指数函数求导在现实生活中有很多应用。比如,在经济学中,我们可以用指数函数来描述人口增长、经济增长等。在物理学中,指数函数可以用来描述放射性物质的衰变。
举个例子,假设一个放射性物质的半衰期是10年,那么10年后,这种物质的数量会减少到原来的一半。如果我们用指数函数来描述这个过程,就可以得到 f(t) = 1/2 e^(t/10),其中 t 是时间(以年为单位),e 是自然对数的底数。
现在,如果我们想知道100年后,这种物质的数量会减少到原来的多少,我们只需要将 t = 100 代入公式,然后求导数即可。
指数函数求导的技巧
虽然指数函数求导的公式很简单,但在实际操作中,我们还是需要一些技巧。
1. 记住公式:这是最基本的要求。只有记住了公式,你才能在需要的时候迅速应用它。
2. 熟练掌握对数:指数函数求导涉及到对数,所以你需要熟练掌握对数的运算。
3. 注意常数 a 的范围:当 a > 1 时,函数是递增的;当 0 < a < 1 时,函数是递减的。这个特性在解决实际问题时非常有用。
指数函数求导的挑战
虽然指数函数求导看起来很简单,但在实际应用中,我们可能会遇到一些挑战。
1. 复杂函数的求导:有时候,我们需要对复杂的指数函数进行求导,这时候就需要运用一些高级的数学技巧。
2. 数值计算:在处理实际问题时,我们往往需要用到数值计算,这时候就需要注意精度和误差。
3. 物理意义:在应用指数函数求导时,我们需要注意其物理意义,避免出现错误的解释。
指数函数求导是一个既神奇又实用的数学工具。通过这篇文章,我希望你能够对这个概念有更深入的了解。记住,数学的魅力就在于它能够帮助我们理解这个世界,解决实际问题。让我们一起,继续探索数学的奇妙世界吧!